Исследование фазовых эффектов в бинарных азеотропных смесях

U= TS-PV+ μ1x1+ μ2x2 2.11

После дифференцирования получаем

dU= TdS + SdT – PdV – VdP + μ1 dx1 + x1dμ1 + μ2 dx2 + x2dμ2 2.12

Но так как

dU= TdS - PdV+ μ1 dx1 + μ2 dx2 2.13

то очевидно

SdT-VdP+ x1dμ1+ x2dμ2 =0 2.14 Если применять почленно преобразование Лежандра, то, учитывая, что при этом меняется в каждом случае знак, получим

-SdT+VdP- x1dμ1- x2dμ2 =0 2.15

Автор [14] не видит разницы между уравнениями в форме 2.14 и 2.15, поэтому приводит уравнение 2.15, очевидно считая, что если правая часть равна нулю, то обе формы идентичны.

Как уже говорилось, нулевой потенциал есть скалярное произведение вектора

< S, V, x1, x2 >

на вектор < dT, dP, dμ1, dμ2 >

Учитывая, что это скалярное произведение равно нулю, векторы-сомножители ортогональны друг другу.

Так как, вектор < dT, dP, dμ1, dμ2 > есть вектор параметров, которые могут изменяться независимо, очевидно вектор < S, V, x1, x2 > может быть представлен двояко < S, -V, x1, x2 > или <- S, V, -x1, - x2 >

Оба представления получаются равнозначными, так как эти векторы ортогональны. Проиллюстрируем это при условии Р=соnst. В этом случае имеем

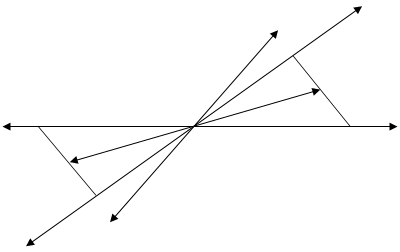< S, x1, x2 > и <- S, -x1, - x2 > S

S х1 х2 х1

х

-х2 х2

-х

-S -х1 -х2

-х1

- S

Рис.2.10. Взаимное расположение вектора состава

То есть, в случае перемены знаков произведение знака не меняет, если давление постоянно.

Выведем уравнение Ван-дер-Ваальса для жидкой фазы. Исходим из того, что в этом случае начальная точка вектора конноды при Р=соnst будет точка, соответствующая свойствам жидкой фазы. В связи с этим правилом запишем уравнения 2.14 для паровой и жидкой фаз при Р=соnst:

Sп dT + у1 dμ1 + у2 dμ2=0 2.16

Sж dT + x1 dμ1 + x2 dμ2=0 2.17

Отнимем от первого уравнение второе и получим:

(Sп- Sж) dT + (у1- х1)dμ1 +(у2- x2)dμ2=0 2.18

Таким образом, мы, получим произведение конноды жидкость-пар < Sп- Sж, у1- х1, у2- x2> на вектор параметров < dT, dμ1, dμ2 >, которые в условиях термодинамического равновесия одинаковы, как в жидкой, так и в паровой фазах.

Так как х1+х2=1 и у1+у2=1, то очевидно

у1- х1+ у2- x2=0

т.е. у2- x2= -(у1- х1) 2.19

Следовательно, с учетом 2.19

(Sп- Sж) dT + (у1- х1) (dμ1-dμ2)=0 2.20

В уравнении 2.20 dT и d(μ1-μ2) полные дифференциалы.

Для перехода к координатам функции g необходимо выразить d(μ1-μ2), как функции х1 и Т (Р=соnst)

d(μ1-μ2) = 2.21

Подставляя в уравнение 2.20 значение d(μ1-μ2) из 2.21, получим

2.22

можно представить в виде . В самом деле, , . Но согласно соотношению Максвелла (смешанные производные не зависят от порядка дифференцирования).