Рабочий пример. Микросостояния атома углерода.

Спин-орбитальный эффект приводит к тому, что термы Рассел-Саундерса расщепляются на несколько подуровней, каждый из которых характеризуется внутренним квантовым числом, принимающим значения . Внутреннее квантовое число J

определяет мо­дуль суммарного момента импульса электронной оболочки, а, соответственно, суммарного магнитного момента атома.

Спин-орбитальный эффект воз­никает в том случае, когда оба из независимых моментов импульса электронной оболочки атома, орбитальный и спиновый не равны нулю. Если же хотя бы один из них равен нулю, то спин-орбитальный эффект не имеет места.

19. Низший из атомных термов на шкале энергии (основной терм) определяется комбинацией трёх пра­вил Хунда. Они следующие:

1-е правило Хунда:

В пределах орбитальной конфигурации основной терм обладает

макси­мальной мультиплетностью.

2-е правило Хунда:

Если в пределах орбитальной конфигурации у нескольких термов муль­типлетность одинакова, то у основного терма орбитальный момент наибольший и квантовое число L

максимальное.

3-е правило Хунда:

Если в пределах орбитальной конфигурации орбитальный подуро­вень заполнен менее, чем наполовину, среди термов, возникающих в результате спин-орбиталь­ного расщепления, низшему отвечает минимальное внутреннее квантовое число J

(нормаль­ный терм), а при заполнении орбитального подуровня более, чем наполовину, низший терм характеризуется максимальным внутренним квантовым числом J

(обращённый терм).

Уточняя символы атомного терма Рассел-Саундерса за счёт включения спин-орбитального эффекта, записывают их в виде . Эти термы отражают схему последовательных приближений в учёте различных сла­гаемых полной энергии коллектива электронов в атомной оболочке в отсутствие внешних силовых полей.

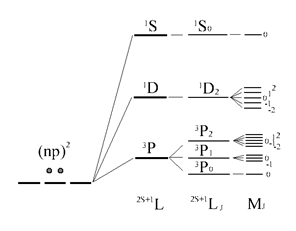
В итоге термы, возникающие в основной конфигурации атома углерода, представлены следующим образом:

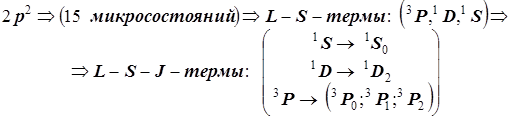
Во внешнем магнитном поле наблюдается дополнительное расщепление атомных уровней по атомному квантовому числу J. С учётом этого расщепления нумерация уровней осуществляется с помощью квантового числа MJ.

В завершение этого раздела приведём последовательность атомных уровней на каждой стадии последовательного уточнения картины взаимодействий .

Последовательность учёта электронных взаимодействий и энергетическая диаграмма атомных уровней (термов) для основной конфигурации np

2 атома C

(или Si

, .)

Существует очень простой приём определения основного терма атомной оболочки (мнемоническое правило Грегори).

Для этого в пределах высшего незавершённого подуровня распределяют электроны с максимально возможным спиновым распариванием. При этом по АО они распределяются таким способом, чтобы достигалось максимальное значение суммарного орбитального момента. В результате получаем микросостояние с экстремальными проекциями M Lmax и MSmax , значения которых совпадают с соответствующими числами L, S основного терма.

ПРИМЕР 1(атом C(p2)). M Lmax=1+0; ® Lmax=2; ® D; MSmax=1/2+1/2; ® Smax=1; ®

® 2Smax+1=3 (триплет) ; Терм 3

D

или точнее C (2p2) 3

D

ПРИМЕР 2(атом Ti(d2)). M Lmax=2+1; ® Lmax=3; ® F; MSmax=1/2+1/2; ® Smax=1; ®

® 2Smax+1=3 (триплет) ; Терм 3

F

или точнее Ti (3d2) 3

F

ПРИМЕР 3(атом Fe(d6)). M Lmax=2; ® Lmax=2; ® D; MSmax=5/2-1/2=2; ® Smax=2; ®

® 2Smax+1=5 (квинтет) ; Терм 5

D

или точнее Fe (3d6) 5

D

ПРИМЕР 4(атом N(p3)) . M Lmax=0; ® Lmax=0; ® S; MSmax=3/2; ® Smax=3/2; ®

® 2Smax+1=4 (квартет) ; Терм 4

S

или точнее N (2p3) 4

S

20. Анализ возбуждённой конфигурации производится по такой же схеме.

Пример 2: Первая возбужденная конфигурация атома Be

(1

s

2

2

s

1

2

p

1

)

.

Микросостояния электронной оболочки атома бериллия в основной и двух последующих возбуждённых конфигурациях: (2s2 ), (2s12p1), (2p2)