Прогнозирование энтропии методом статистический термодинамики

В тех случаях, когда это предусмотрено решаемой задачей, рассчитывается вклад в энтропию, обусловленный смешением конформеров. Программой Entropy наряду с классическим подходом предусмотрен следующий вариант расчета энтропии смешения конформеров. На основании полученных ранее сведений об изменении энергии молекулы при вращении каждой из ее групп вычисляется

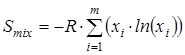, (2.18)

где m – общее количество рассматриваемых конформаций (в нашем случае учитывались все состояния, полученные при повороте волчка от 0о до 350о с шагом 10о, то есть m=36∙n, где n – число вращающихся групп в молекуле), xi – мольная доля каждой конформации

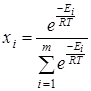, (2.19)

где n – число вращающихся групп в молекуле, m – количество рассматриваемых конформаций, Ei – энергия молекулы, в данном состоянии равная , где - исходное значение энергии, - наименьшая энергия молекулы, полученная при вращении всех возможных волчков.

Для нахождения вклада в энтропию, обусловленного колебательным движением, используются расчетные значения частот колебательного спектра, рассчитанные любым из квантово-химических методов, реализованных в программах Gaussian или Hyperchem, для оптимизированной тем же методом геометрии молекулы. Критерием качества оптимизации служит отсутствие в спектре отрицательных значений частот.

Расчет вклада в энтропию, обусловленного колебательным движением, производится следующим образом.

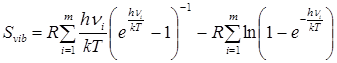, (2.20)

где νi – частота из принятого к расчету набора, m – количество частот в наборе. Из полного набора частот колебательного спектра исключаются крутильные колебания, соответствующие вращению групп, участвующих в расчете вклада в энтропию от заторможенного вращения; таким образом, , где n – число атомов в молекуле, ntop – число волчков. При отсутствии надежных методик определения крутильных колебаний в спектре применяется приближенная оценка типов колебаний с использованием режима Animate программы HyperChem 5.0.

Информация о геометрии молекулы и потенциальных кривых барьеров вращения волчков используется для расчета вклада в энтропию, обусловленного внутренним вращением групп в молекуле. Энтропийный вклад определялся как

, (2.21)

здесь n – число максимумов потенциальной кривой барьера вращения группы, s– число симметрии группы (подходы к определению чисел симметрии вращающихся групп рассмотрены выше), Sfr – энтропия свободного вращения волчка, - разность между энтропиями свободного и заторможенного вращения, определяемая по таблицам Питцера и Гуинна [1] как функция и , где Vo – эффективный барьер вращения волчка, Qfr – статистическая сумма по состояниям свободного внутреннего вращения.

Величина эффективного барьера вращения принимается равной 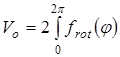, где - зависимость изменения потенциальной энергии молекулы от угла поворота волчка φ. Для расчета Vo полученные методом молекулярной механики значения потенциальной энергии молекулы при заданных значениях угла поворота волчка описываются с помощью кубического сплайна, затем полученный сплайн интегрируется по методу Симпсона.

Статистическая сумма по состояниям свободного внутреннего вращения рассчитывалась как

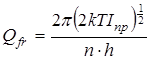, (2.22)

где Iпр – приведенный момент инерции волчка, который рассчитывался в соответствии со следующей процедурой.

Для вращающейся группы вводится координатная система с осями x, y, z, расположенными следующим образом: ось z совпадает с осью вращения волчка, ось x проходит через центр масс волчка и перпендикулярна оси z, ось y проходит через точку пересечения осей x, z и перпендикулярна к ним. Атомы волчка, лежащие на оси z, из дальнейшего рассмотрения исключаются. Далее производится расчет следующих величин: - момент инерции волчка относительно оси z, и - произведения моментов инерции, - фактор несбалансированности волчка.

Затем находятся направляющие косинусы осей x, y, z относительно главных центральных осей 1, 2, 3 инерции молекулы. Направление осей выбирается таким образом, чтобы обе системы координат были или правыми, или левыми. При этом должно соблюдаться условие равенства единице определителя матрицы направляющих косинусов, т.е.