Теория возмущений в приближении граничных МО

Из правила БЭП следует, что знание энергетического состояния исходных

и конечных

продуктов позволяет оценивать кинетические характеристики ЭС (вероятность реализации элементарного акта). Метод возмущения МО (МВМО), оперируя только граничными занятыми и свободными МО (ВЗМО, НСМО) и зарядами (на атомах в молекулах и на атомных орбиталях в МО) в исходных

реагентах, позволяет в ряде случаев предсказать вероятность, направление и эффективностьвзаимодействия двух реагентов.

Чем эффективнее взаимодействие, тем ниже Еакт и тем выше вероятность согласованного (элементарного) акта.

Если энергии граничных орбиталей c1 и c2 близки, то энергия взаимодействия определяется резонансным (обменным) интегралом b12

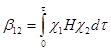(28)

где H – гамильтониан системы, t – элемент объема, в котором происходит перекрывание орбиталей. Величина b12 в этом случае определяет и величину расщепления новых МО Y1 и Y2 или энергию стабилизации e = b12.

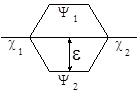
Если энергии c1 и c2 различаются сильно, то величина e определяется не только b12, а зависит и от разности энергий c1 и c2 по уравнению (29):

(29)

где Е1 и Е2 – энергии низшей и высшей МО

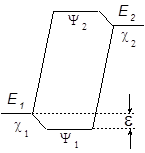
Чем больше величина e , тем стабильнее образующийся аддукт, тем ниже Еакт его образования.

МВМО не дает оценки Е переходного состояния и Еакт. Рассчитывается лишь разница между полной электронной энергией реагирующей системы Е и энергиями исходных реагентов и (малое возмущение):

DЕ = Е – – , (30)

справедливое только для начальных участков координаты реакции. Только на больших расстояниях между реагентами не происходит смешения МО, нет межмолекулярного отталкивания и можно говорить о чистых МО исходных реагентов. Вместе с тем, такое приближение позволяет оценить наиболее вероятный путь реакции.

Энергию возмущения DЕ при взаимодействии реагентов S и Т (S и Т – молекулы или активные центры в молекулах) рассчитывают по уравнению 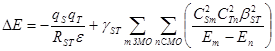(31):

(31)

В случае только двух граничных МО (например, молекул донора и акцептора) уравнение упрощается 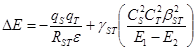(32):

(32)

В уравнениях (31, 32) qS и qT – эффективные заряды на центрах S и Т, RST – расстояние между центрами в ходе взаимодействия, e – диэлектрическая проницаемость среды. Таким образом, первый член (возмущение 1го порядка) отражает энергию кулоновского взаимодействия. Второй член (возмущение 2го порядка) определяет энергию орбитального перекрывания и включает: gST – коэффициент, учитывающий заселенность электронами орбиталей c1 и c2, и – квадраты коэффициентов при атомных орбиталях центров S и Т волновой функции граничных МО c1 и c2, – квадрат обменного интеграла, Е1 и Е2 – энергии орбиталей c1 и c2. Разные случаи заселенности орбиталей c1 и c2 реагирующих частиц и коэффициент gST приведены ниже: