Теория активированного комплекса (ТАК)

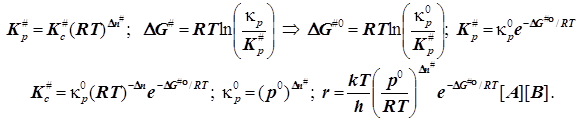
Внимание! Отсюда следует выражение для константы скорости бимолекулярной реакции в ТАК, не вызывающее сомнений в размерности констант скоростей бимолекулярных реакций:

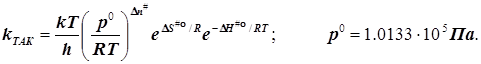(6.2)

В учебниках чаще всего приводится не столь прозрачное выражение, построенное на иной стандартизации состояний - стандартизуют концентрацию, и в итоге возникает размерность константы скорости, внешне соответствующая моно-, а не би молекулярной реакции. Размерности концентраций оказываются как бы скрыты. У Эйринга, Глесстона и Лейдлера - самих творцов ТАК в книге «Теория абсолютных скоростей реакций» есть анализ, где учтена стандартизация состояний по давлениям. Если стандартным считать состояние с единичными концентрациями реагентов и продуктов, то формулы слегка упростятся, а именно:

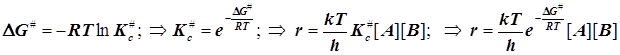Отсюда следует обычно представленное в учебниках выражение для константы скорости согласно ТАК: (6.3)

Если не выделить роль стандартного состояния, то теоретическая константа скорости бимолекулярного превращения может обрести чужую размерность, обратную времени, которая будет отвечать мономолекулярной стадии распада активированного комплекса. Активационные величиныS#0 и H#0 нельзя считать обычными термодинамическими функциями состояния. Они не сопоставимы с обычными характеристиками пробега реакции уже потому, что методов их прямого термохимического измерения просто не существует . По этой причине их можно назвать квазитермодинамическими характеристиками процесса активации.

При образовании частицы активированного комплекса из двух исходных частиц имеет место , и в результате получается

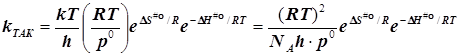(6.4)

Размерность константы скорости обычная для реакции второго порядка:

Эмпирическая энергия активации по Аррениусу и её сравнение с близкими

аналогичными активационными параметрами (энергиями) ТАС и ТАК:

Основа - уравнение Аррениуса в дифференциальной форме:

1) в ТАС получаем:

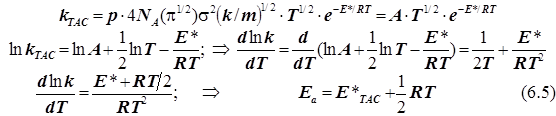
2.1) ТАК. Случай 1. (Общий подход при условии стандартизации концентраций)

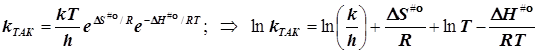
подстановка в уравнение Аррениуса даёт

2.2) ТАК. Случай 2. (Частный случай бимолекулярной стадии активации ).

Энергия активации по Аррениусу для бимолекулярной реакции:

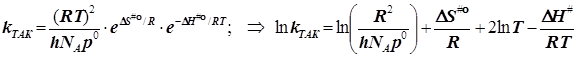
Внимание!!! Полагаем чаще всего

2.2) Исходя из стандартизации давления, получаем энергию активации:

(6.7)

2.3) Это же получается для бимолекулярной реакции и при стандартизации концентрации:

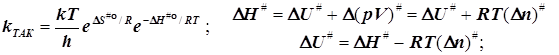(6.8)

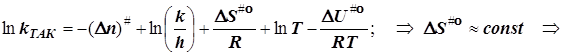
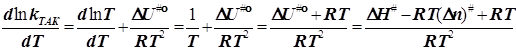
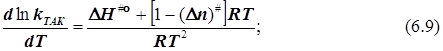
в бимолекулярном акте активации n#= -1, и (6.10)

Результат: Формула, связывающая энергию активации Аррениуса с квазитермодинамическими функциями активации теории переходного состояния, не зависит от выбора стандартного состояния.

3. Адиабатические потенциалы и потенциальные поверхности.