Инновационный путь развития технологии создания новых лекарственных средств

,

где k — константа Больцмана.

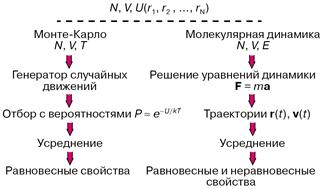
Рисунок 2 – Схема расчетов методами Монте-Карло и молекулярной динамики

При моделировании в рамках молекулярной динамики положения r(t) и скорости v(t) каждой частицы в момент времени t определяются как решения системы уравнений классической механики (уравнений Ньютона) либо уравнений, в которых к силам F задаваемым потенциалом U, добавляются так называемые случайные силы. Макроскопические свойства рассчитываются при усреднении по положениям и скоростям молекул.

Как уже упоминалось, число частиц при моделировании методами Монте-Карло и молекулярной динамики с помошью современных суперкомпьютеров может достигать колоссальных величин. Даже без суперкомпьютеров достаточно типичны численные эксперименты для значений N порядка десятков и сотен тысяч. Примеры успешного применения методов Монте-Карло и молекулярной динамики для моделирования равновесных составов смесей при постоянном давлении, фазовых равновесий, адсорбции на поверхности твердых тел, свойств жидкостей в микропорах и т.д. достаточно многочисленны. Этими же методами решаются задачи поиска устойчивых конформаций (поворотных изомеров) полимерных молекул, чрезвычайно важные для биохимических приложений [5,6].

Рассмотрим достаточно последовательную квантовую модель на примере бимолекулярной реакции типа

Х(i) + Y(j) → Х'(i') +Y'(j') + …

Здесь предполагается столкновение двух молекул X и Y, находящихся в состояниях i и j соответственно, которое приводит к продуктам реакции, то есть к молекулам X', Y', . в квантовых состояниях i', j', . Квантовая теория столкновений в принципе позволяет вычислить вероятности переходов между состояниями, отвечающими реагентам и продуктам, затем найти парциальные, то есть относящиеся к данным наборам квантовых чисел (здесь i, j, i', j', .), константы скорости. При усреднении по квантовым состояниям реагентов и продуктов можно оценить макроскопическую константу скорости соответствующей газофазной химической реакции как функцию температуры.

Полное осуществление этой программы в конкретных приложениях крайне затруднительно, даже если из предшествующих квантово-химических расчетов известна поверхность потенциальной энергии. Самой сложной стадией является численное решение уравнений квантовой теории столкновений с учетом перераспределения частиц, то есть как раз наиболее важная для химии стадия. Следует, однако, подчеркнуть исключительную важность научных исследований в этом направлении, поскольку они формируют каркас обшей теории, с которой сравниваются более простые модели. Кроме того, современные экспериментальные методы исследования динамики молекул позволяют измерить парциальные константы скорости и непосредственно сопоставить экспериментальные и теоретические результаты.

Более простые, а потому и более практичные способы вычисления констант скорости химических реакций получают обычно при определенных упрощениях полной квантовой модели. Так, начиная с 50-х годов проводятся компьютерные расчеты скоростей реакций методом классических траекторий. В этом методе, как и ранее, предполагается разделение электронной и ядерной подсистем, но в данном приложении необходимо знание поверхностей потенциальной энергии для достаточно широких интервалов межъядерных расстояний. Для расчета движений ядер, совместимых с данной потенциальной поверхностью, решают уравнения классической механики, а оценки констант скорости получают при сопоставлении числа траекторий, приводящих к реакции, с исходным числом траекторий при статистическом задании начальных условий.