Теория Активных Соударений (ТАС)

2.1.1. Число двойных соударений между одинаковыми частицами

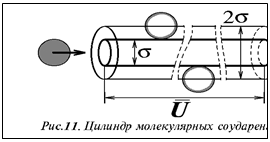
Одна частица в единицу времени пробежит «цилиндр соударения» (рис.), в котором затронет любую частицу, центр которой в него попадает, и его объём выражается через среднюю скорость частицы u и её диаметр :

(5.6)

Число частиц в этом цилиндре пропорционально его объёму и мольной концентрации. С ними-то и сталкивается одна частица. Полное же число столкновений в единичном объёме Z’ должно бы быть равно половине от произведе­ния числа соударений одной частицы на число всех частиц в объёме (удобно выразить его через мольную концентрацию), но, согласно газокинетической теории Максвелла, истинное число соударений Z превышает Z’ в 21/2 раз из-за ломаного характера траектории, увеличивающего вероятность встреч частиц в пространстве. Необходимые формулы имеют вид:

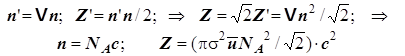(5.7)

Примечание: Неискушённый читатель вправе удивиться столь простому и решительному способу подсчёта числа столкновений частиц – ведь, всякое соударение изменяет вектор скорости, и реальная траектория это ломаная линия. Однако учтём, что при упругом ударе изменяется лишь направление, а не модуль вектора скорости, и поэтому длина ломаной траектории, образуемой за единицу времени, остаётся равной линейной скорости частицы. Это подобно тому, как длина столярной складной линейки суммируется из её отдельных сегментов. Полезно отметить, что и уточнение числа соударений за счёт учёта постоянной смены ориентации движений, носит формальный характер, не меняя существа дела. Добавим, что газокинетический диаметр частиц понятие до известной степени условное и вводится для упрощения модели.

2.1.2. Число соударений между разными частицами (частицы вида 1 и частицы вида 2)

В формулу средней скорости следует подставить усреднённый диаметр и приведённую массу, и также нет необходимости уменьшать число соударений вдвое. Все прочие соображения те же самые . Поэтому при наличии всех сомножителей со слегка изменённым смыслом численный множитель возрастёт вдвое . Действительно, получаем

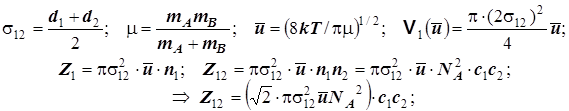(5.8)

2.1.3. Число «горячих» частиц одного вида равно , откуда получаем:

1) число «горячих» соударений между молекулами одного вида

(5.9)

2) число «горячих» соударений между молекулами разных видов

(5.10)

2.1.4. Бимолекулярные элементарные акты. Два различных случая

1) Реагируют одинаковые частицы:

(M- частицы продукта )

Скорость первой стадии это число «горячих» частиц, образующихся в единицу времени, и, согласно стехиометрии, оно равно числу активных соударений. Это означает:

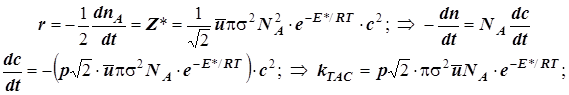(5.11)

2) Реагируют различные частицы:

(M – частицы продукта)

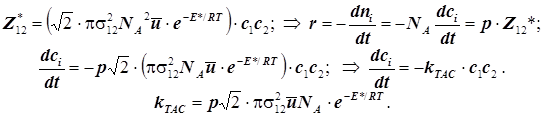(5.12)

Получена та же формула, что и для реакции одинаковых частиц. Здесь эмпирический поправочный множитель p называется стерическим фактором. Он характеризует отклонение от теоретического значения под влиянием любых факторов. Принято считать, что он возникает из-за поправок на вероятность встречи молекул своими активными регионами – теми, где находятся их реакционные центры.

Комментарий. Элементарные сведения из молекулярно-кинетической теории:

Средние скорости частиц идеального газа и их пропорция в распределении Максвелла:

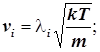
и

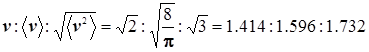
(скорости: наиболее вероятная, средняя арифметическая, среднеквадратичная ). В принципе-то их отличия несущественны, и строго говоря, неважно, какую из них использует читатель Всё равно в приложениях далее появляется эмпирический поправочный стерический фактор, который обычно на многие порядки может отличатся от единицы .