Расчёт многокорпусной выпарной установки

Вт/(м2∙К)

Тогда получим:

град

град

Вт/(м2∙К)

Вт/м2

Вт/м2

Очевидно, что q’ ≠ q”. Для расчёта в третьем приближении строим графическую зависимость удельной тепловой нагрузки q от разности температур между паром и стенкой (рис. 4) и определяем Δt1.

Рис. 4. График зависимости удельной тепловой нагрузки q от разности температур Δt1

Согласно графику можно определить Δt1 = 3,2 град. Отсюда получим:

Вт/(м2∙К)

град

град

Вт/(м2∙К)

Вт/м2

Вт/м2

Как видим, q’ ≈ q”. Так как расхождение между тепловыми нагрузками не превышает 3%, на этом расчёт коэффициентов α1 и α2 заканчиваем и находим К1:

Вт/(м2∙К)

Далее рассчитываем коэффициент теплопередачи для второго корпуса К2. Примем в первом приближении Δt1 = 2,0 град. Для определения К2 найдём:

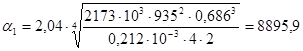Вт/(м2∙К)

град

град

Вт/(м2∙К)

Вт/м2

Вт/м2

Как видим, q’ ≠ q”. Для второго приближения примем Δt1 = 5 град, пренебрегая изменением физических свойств конденсата при изменении температуры, рассчитываем α1 по соотношению:

Вт/(м2∙К)

Тогда получим:

град

град

Вт/(м2∙К)

Вт/м2

Вт/м2

Очевидно, что q’ ≠ q”. Для расчёта в третьем приближении строим графическую зависимость удельной тепловой нагрузки q от разности температур между паром и стенкой (рис. 5) и определяем Δt1.

Рис. 5. График зависимости удельной тепловой нагрузки q от разности температур Δt1

Согласно графику можно определить Δt1 = 2,2 град. Отсюда получим: